In his classic work,
Proofs and Refutationas, Imre Lakatos explored how mathematics develops in practice.
He choose as his model for study the evolution of proofs published in
the mathematics literature, both in papers and texts,
of the proof of Euler's Formula, that relates
- E = the number of edges
- V = the number of vertices
- F = the number of faces
for three dimensional polyhedra according to the equation
V + F - E = 2
This formula is very easily checked for the five platonic solids
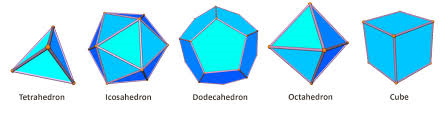
| V=4 | V=12 | V=20 | V=5 | V=8 |
| F=4 | F=20 | F=12 | F=6 | F=6 |
| E=6 | E=30 | E=30 | E=9 | E=12 |
and it works perfectly for familiar convex polyhedra.
Latatos showed how with the discovery of various counter-examples --
polyhedra for which Euler's Formula does not hold --
the published "proofs" of Euler's Formula, evolved over time.
These counter-examples were termed by Lakatos monsters.
Lakatos delineated two major procedures for dealing with
monsters:
- monster-barring
- monster adjustment
as well as what he termed exception barring.
Most striking of the monsters that Lakatos discussed were
| 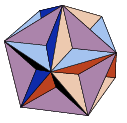
The Great Dodecahedron |
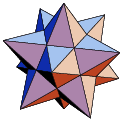
Small Stellated Dodecahedron |

The Nested Cube
[ Wireframe ] |
| V=12 | V=12 | V=16 |
| F=12 | F=12 | F=20 |
| E=30 | E=30 | E=32 |
| V+F-E=-6 | V+F-E=-6 | V+F-E=4 |
[ Note the use of specific colours for each visible face of the monstrous dodecahedrons ]
The original articles and the 1976 book by Lakatos, Proofs and Refutations are not freely available online.
However this writer recommends for academic readers two online publications:
 and and  An Examination of Counterexamples
in Proofs and Refutations
An Examination of Counterexamples
in Proofs and Refutations
Jesse Lambe Formal Proofs and Refutations, PhD thesis, Stanford, 2009
Now it must be said that while Lakatos was solely concerned with the historical development of proofs in pure mathematics.
here his terminology has been applied by me to the description
of problem solutions in qualitative physics.
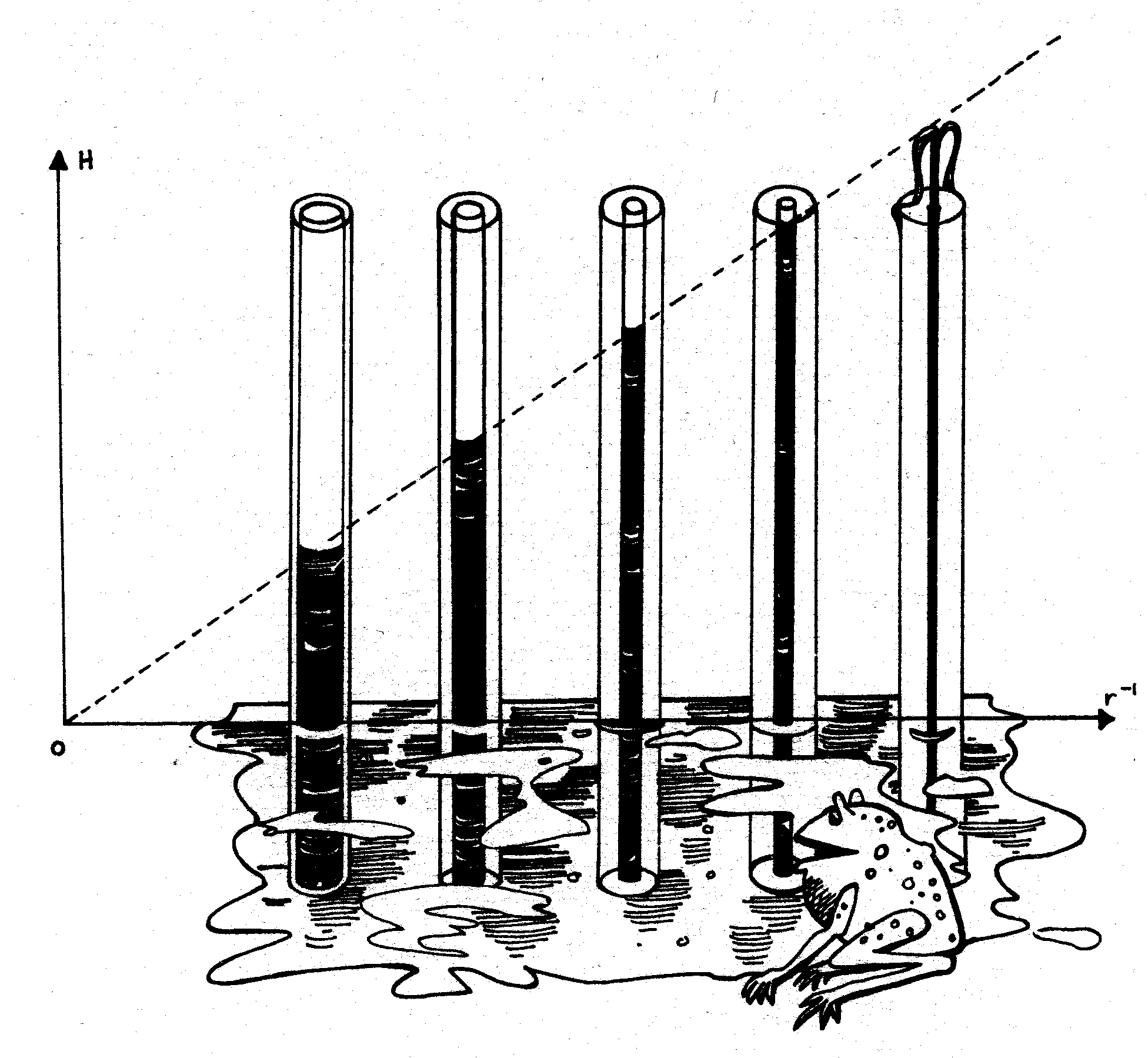
|
Elementary physics solution:
Water in a vertical capillary tube immersed in water
will rise an amount
H = K/r
Derivation as per many texts
For surface tension T, and angle of contact
θ a column of water (or like fluid) will be rise by amount H till the gravitational force on the
column (above surroundings)
is matched by the total surface tension, so that
2πrTsin(θ) = π r2 ρg H
where ρ is the fluid density, and g is the force of gravity.
Hence, introducing a constant K, the rise in the tube is computed as
H = K/r
|
In presenting this graphic Inducia Capillaria to a wide range of subjects
I have added verbal reparté such as:
One sees that the narrower the tube -- the higher the water roses. Does that
mean that for a thin enough tube water would spray out of the top of the tube?
Or would water just dribble over the top of the tube?
|
 The Gecko -- is the most intriguing of Dragons. Colourful but bereft of eyelids,
lacking claws, yet so provocative. Aristotle insisted that the gecko
can run up and down a tree in any way, even with the head downwards.
Its physics --
how the gecko climbs walls and even across ceilings -- is beyond Aristotle and Newton -- and involves quantum physics.
[ Not that such advanced physics is required to dissect and analyse my geckos.]
When challenged by a gecko many try to bar this creature --
but the more creative task is to "tame" [adjust] the gecko
so as to transform it to
something more familiar. The genus was properly first described in problem-solving terms by Imre Lakatos, hence
the alternate nomenclaure Lakatosian Monster.
The Gecko -- is the most intriguing of Dragons. Colourful but bereft of eyelids,
lacking claws, yet so provocative. Aristotle insisted that the gecko
can run up and down a tree in any way, even with the head downwards.
Its physics --
how the gecko climbs walls and even across ceilings -- is beyond Aristotle and Newton -- and involves quantum physics.
[ Not that such advanced physics is required to dissect and analyse my geckos.]
When challenged by a gecko many try to bar this creature --
but the more creative task is to "tame" [adjust] the gecko
so as to transform it to
something more familiar. The genus was properly first described in problem-solving terms by Imre Lakatos, hence
the alternate nomenclaure Lakatosian Monster. 






