The By Pass Strategy in Simple Maths Smith, diSessa, and Roschelle report in a study involving both maths novices and relative experts confronted with the teaser above that: A frequent strategy for comparing 8/11 and 7/15, for example, was to assert that the common reference number, 1/2, was between 8/11 and 7/15 and to use that order relation to infer that 8/11 > 7/15. See their paper for details:    John P. Smith, Andea A. diSessa, Jeremy Roschelle, Misconceptions Reconceived: A Constructivist Analysis of Knowledge in Transition Downloadable The reportage by Smith et al is all too brief. Implicit is that the respondents somehow decided that 1/2 was a useful reference, and that       8/11    >   1/2   and    1/2   >  7/15 whence           8/11   >   7/15 This writer himself most deliberately used the By Pass Heuristic - my solution using the different intermediate state of 7/11 so that       8/11    >   7/11   and    7/11  >  7/15 whence           8/11   >   7/15 In my solution there is a progressive shift of the numerator of the first fraction towards that of the second -- and not the arbitrary selection of an entirely new number - the 1/2. Just what ideas drove the respondents of Smith et al quiz to chose 1/2 as the "reference number" ? 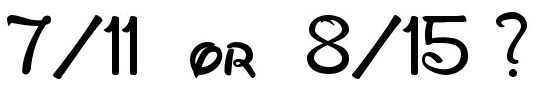This could have been explored by Smith et al by posing related fraction inequalities such as where 1/2 is not a "good" reference number Enquiries discussion email aboutdragonsATtpg.com.au {Replace the AT by @ in your mail program.