Heuristics and the Growth of Intelligence
The aim of these pages is to sketch out a thesis on the nature of cognive growth via examples
of problem-solving in action.
Whilst I was a member of the MIT AI (Artificial Intelligence) Lab in 1974/5 I had the opportunity to sit in while one of Piaget's research students conducted interviews with children 4-7 years in a Lexington school. In these interviews, the children were asked qualitative questions about quantity called Piaget's Conservation Puzzles.
The Egg Cup Game -- A Piagetian Conservation Puzzle
:
In order to answer questions as to whether some quantity is greater or less than another, the typical child uses such heuristics as:
- H0: If two sets are "matched" one-to-one then quantity is "The Same"
- H1: Greater extent means more.
- H2: Sparseness (greater gaps between elements) means less.
- H3: Counting tells you if more or less.
The heuristic H3 is only suitable for very small sets because of a (young) child's limited skill at counting. The sorts of situations where a typical child of five years gives the correct answer to questions about quantity are shown in Fig (xvi) of Reference (1), A being what we term a paradigm for H1, while B gives two paradigms for H2. It is a notable about these paradigms that only one heuristic is applicable to each. But what happens if a situation is presented to which both heuristics are applicable, and give conflicting conclusions? In one of the classic "conservation" experiments of Jean Piaget, the egg-cup experiment, children in the 4-7 years age group are set such a clash in their heuristics.
The students were shown a collection of eggs in egg-cups, one in each cup. After questioning, each egg was removed from its cup, and the eggs spread out to a greater extent than the egg-cups, all this whilst the child watched. Here is the story in pictures:
 :
:
In summary, if children are shown a line of eggs in egg-cups, where the extent and sparseness of both the eggs and the egg-cups are the same, then in answer to the question "Are there more eggs or more egg cups?" the typical child (4 - 7 years) answers "no the same." However, if the set-up stays in full view of the child while the eggs are removed from the egg cups and spread out in a longer line than the line of the cups - then the situation is one in which H1 and H2 give conflicting assessments to the repeated question. However, for the young child, H1 is in some way tagged as primary or more important - - for, as indicated below, H1 describes a great range of situations where such evaluations are sought. So the typical five year old will now reply, "More eggs". In contrast the seven year old will give the adult answer "Of course not." What distinguishes the seven year old from the typical five year old? Possibly the seven year old has acquired a heuristic such as:
-
H4: Relationships "more than" or 'less than" remain true if items are moved but not removed
However, the mere addition of H4 to a child's repertoire won't necessarily lead to the correct answer to the repeated question of the egg and egg-cup experiment. What is needed is some caveat like
- H5: In case of conflict between H1 and H2 use H4
The addition of these - - or somesuch - - heuristics to the heuristic that holds the collection H1, H2, etc of the typical five year old child is an instance of cognitive growth.
Piaget's Conservations puzzles for children 4 -7 year
s old are analogous to the Dragons in the compilation
Harvey A. Cohen, A Dragon Hunter's Box, not only in that the "solutions" presented sharply distinguish beginners from relative experts -- but in the fact that one can observe the same heuristics in use.:
5 year uses Process in context of Piagetian 'Conservation" Experiment
Here is the protocol of classic Piagetian "conservation" experiment, conducted by one of Piaget and
Inhalder's collaborators, Olivier de Marcellus, in Lexington, Massachusetts in September, 1974.
A five year old child Rob [name altered] was shown two vessels. One, a measuring cylinder, was tall and narrow in cross-section, the other was a squat beaker containing a dark liquid termed "Pepsi". Rob was asked to what height he anticipated the "Pepsi" poured from the beaker would fill the narrow cylinder.
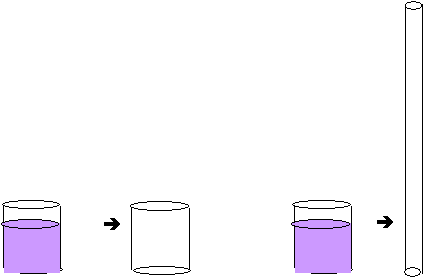
Rob pointed to a level on the cylinder at the same height *(1) as the top level of the "Pepsi" in the squat vessel. The "Pepsi" was poured into the cylinder. The level in the narrow cylinder was about three times higher than that predicted by Rob. Rob registered much astonishment, followed by a traditiona; facial expression for grasping a tricky idea. Rob was asked: "Is these more Pepsi now?". Rob replied, "No! It's just the same . . . . it only looks more". *(2).
Rob was then asked how he would explain to another child how it was that "Pepsi" was so high in the (narrow) cylinder. Rob pondered a moment - - then placed his hands about 20 centimeters apart in front of him, then steadily drew his hands together while saying, "The sides are pushing the Pepsi up" *(3). Rob's responses *(1), *(2), *(3) of the above protocol, merit these comments:
*(1) Rob's expectation of the height of the new (narrow) Pepsi column conforms to the heuristic H1 of the preceding experiment. The anticipated extent of the new Pepsi column - - its height - - was anticipated to be unchanged.
*(2) Rob opined a caveat to be referred to as H6 which he probably only recently learnt to associate with the heuristic H1
- H6: Sometimes it only looks more.
· Rob's response "The same" was undoubtedly guided by heuristic H4 or some similar historical heuristic. Rob was clearly on "the cusp" of becoming a conserver in Piagetian terms.
*(3) Rob was considering a fictitious state of the cylinder - - presumably one in which the cross-section was the same as in the squat beaker. In the fictitious state, the Pepsi would be at the same level as in the squat beaker. But on bringing the sides closer together - - as indicated by Rob's hand movement - - the Pepsi level would rise.
Process
The Process Heuristic is a bundle of problem solving ideas based upon the following scheme:
Look on the situation as a change from initial state A to final state B. Invent some fictitious state C, for which changes from A to C and from C to B can both be easily found.
What was remarkable about Rob, was that he had formulated his explanation (3) in terms of the Heuristic Process.
In fact, the very same day as I observed Rob's Process attack
-- and his hand movements in saying "The sides are pushing ther Pepsi up"
I observed an MIT professor give a Process
solution to the Milko Dragon (that's detailed in Reference [1]);
and the MIT professor used his hands in like manner to open up (straighten) and reform the milk
bottle to cylinder form.
Like so:
For a detailed discussion go to the
Process Approach to the Milk Bottle Problem
This double experience highlighted the fact that not only an experienced academic computer scientist/mathematician,
but even a child as young as Rob could apply the Process
heuristic. Clearly both had the same core idea for Process.
But the MIT professor had developed the heuristic
to incorporate greater adaptability.
REFERENCES
-
Harvey A. Cohen, The Art of Snaring Dragons, M.I.T. Artificial Intelligence
Laboratory Memo 338, No 338, May 1975.
Downloadable as PDF

-
Andrea di Sessa and Bruce L. Sherin, What Changes in Cognitive Growth,
International Journal of Science Education,
20(10), 1155-1191 (1998)
- J. Piaget, The Child's Concept of Number, Norton, New York (1965); J.Piaget and B.Inhelder, The Child's Concept of Space, Norton, New York (1967).


