Process Approach to Milk Bottle Problem

The Process Heuristic is a bundle of problem solving ideas based upon the following scheme:
Look on the situation as a change from initial state A to final state B. Invent some fictitious state C, for which changes from A to C and from C to B can both be easily found.
In a "Process" analysis of the Dragon Milko. where one perceives this Dragon as involving a transformation State Aâ State B where

State A: Homogenous milk in milk bottle. with base pressure p[A] = p
State B: Stratified milk in milk bottle. with base pressure p[B] = p'

One can't compute the alteration in base pressure - - i.e., p[A] - p[B] = p - p' directly - - after all, this is the problem of this Dragon. Yet if the neck of the milk bottle was rubber, or was hinged somehow, and the bottle transformed into a cylinder it would be easy, in fact trivial, to compute the base pressure change after stratification by reference to the states:

State X: Homogenous milk in cylinder with base pressure p[X]
State Y: Stratified milk in cylinder with base pressure p[Y]

In a cylinder the only vertical forces acting on the fluid contents (of total weight W) are gravity and the base pressure acting over the area A, so that as X â Y
p[X] = p[Y]
In detail, both pressures are equal to W/A.
The additional base pressure in State A compared to State X is due to an additional height D of milk so that under the transformation
Aâ X : p[A] - p[X] = p - W/A = Dg*density(milk) Likewise
Y â B : p[Y] - p[B] = W/A - p' = Dg*density(cream)
Hence

p - p' = p[A] - p[B] = Dg*{density(milk) - density(cream)}
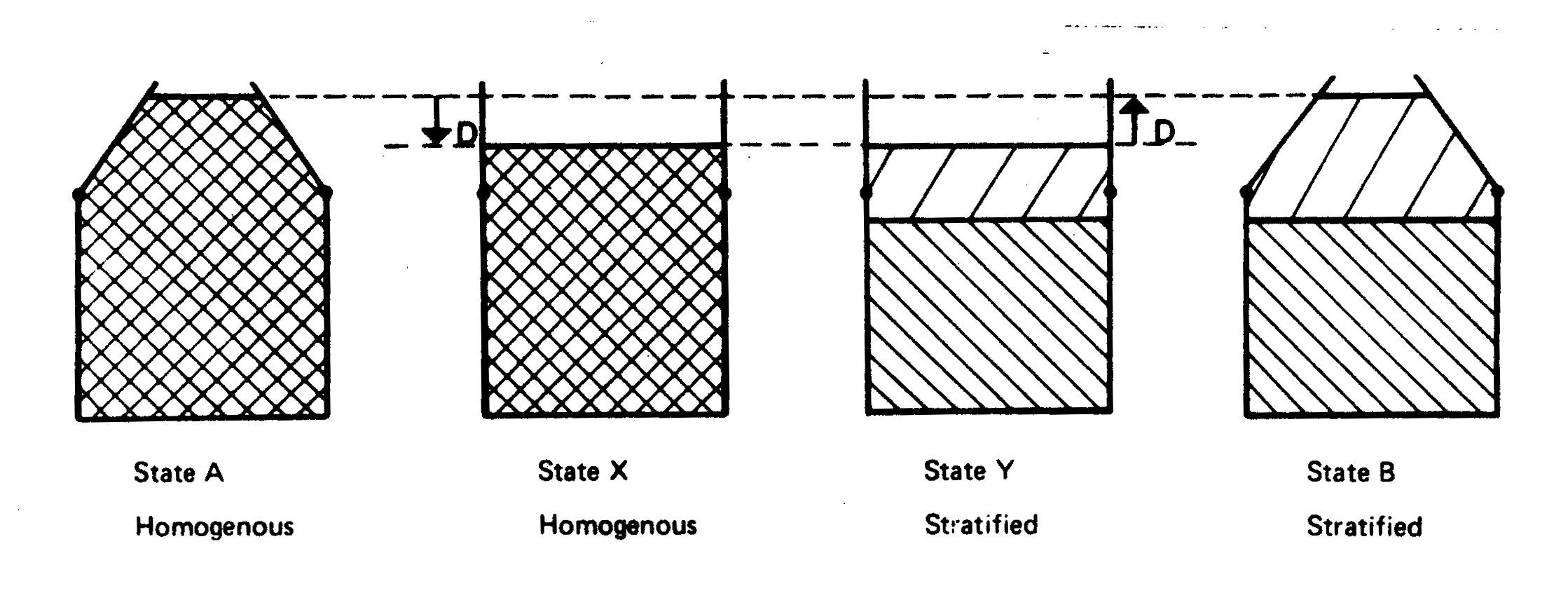
which is positive as cream density = density(cream) is less than the density(milk). This "Process" argument is illustrated in the diagram:

p - D

p - D + d

Looking at this diagram -- one realises that one doesn't need to do any mathematics at all, to deduce that the pressure decreases.
At the first step, A â X, the height of milk drops, so that pressure decreases a lot, from p to p - D Going from State X to Y, X â Y, the base pressure is not altered. But at the final step, Y â B, there is a increase in pressure, as cream is pushed up -- of amount d, but d < D since cream is light.
So one deduces that the final pressure is
p - D + d
less than the initial.

The discussion above is deliberately stylised. Its worth reading the transcript of the interview where I first recorded a Process attack on Milko, which is included, along with some related transcrips, under the heading "The Milk Game"

For other ways to snare Milko, and for related pages, link to:

	Milko via In Toto
	Process Approach to The Coin Problem
	The Art of Snaring Dragons
	Return To Dragons Homepage