Using In Toto to Solve Milko aka The Milk Bottle Problem

To solve this problem using In Toto, one needs to know that

• Pressure increases with depth
• Pressure at a given depth in a uniform liquid depends of the liquid density
• The Pressure exterts a force normal (i.e., perpendicular) to the surface
• The reaction force -- being equal and opposite -- is normal to the containing walls

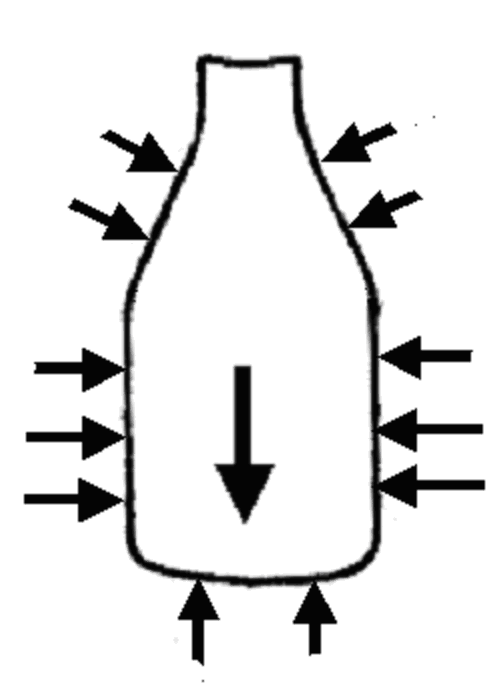
We now ready to take the In Toto approach to the equilibrium of the milk in the bottle. Applying In Toto to the Milk Bottle Problem, we consider the total volume of milk in total, and consider the equilibrium of the milk (before and after separation). Both before and after, there is a gravitational force W acting downwards on the milk, equal to the (unchanged) total weight. This is balanced by the sum of all the reaction forces acting the milk. Now the sum of the horizontal components of the sidewall forces must be zero -- and obviously these horizontal components cancel each other because of the radial symmetry of a milk bottle. But clearly, along the sloping sides of the bottle, the vertical components on opposite sides of the bottle add together, to produce a net downward force which we call X, in the case of homogenous milk, and X' in the case of separated.

Homogenous Milk

But how does X' relate to X ? As cream is less dense than homogenised milk, it follows that the pressure at any depth within the cream is less than that at the same depth in homogenised milk. Hence each little contribution of wall reaction force along the slanting sides (above the cream line) is less in the separated cases than it was before separation. X' < X

Milk Separated, with cream on top

Now the total base force, in terms of area A and base presure p, is balanced by the other vertical forces:

Before	pA = W + X
After	p'A = W + X'
Hence	p'A < pA
and one deduces	p' < p

The base level pressure drops after separation.

	Solving Milko using the Process heuristic
	Milko The Milk Bottle Dragon
	The Art of Snaring Dragons
	Dragon Home Page