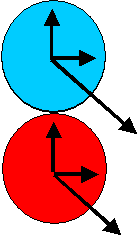
 Fix a reference frame in the centre of both the blue AND the red coins.
Call the diameter of a coin D.
Then in both cases set the z-axis perpendicular to the plane of the coin, and make the
x-axes horizontal (to the screen).
Fix a reference frame in the centre of both the blue AND the red coins.
Call the diameter of a coin D.
Then in both cases set the z-axis perpendicular to the plane of the coin, and make the
x-axes horizontal (to the screen).
Einstein's Solution to the Coin Problem
 Fix a reference frame in the centre of both the blue AND the red coins.
Call the diameter of a coin D.
Then in both cases set the z-axis perpendicular to the plane of the coin, and make the
x-axes horizontal (to the screen).
Fix a reference frame in the centre of both the blue AND the red coins.
Call the diameter of a coin D.
Then in both cases set the z-axis perpendicular to the plane of the coin, and make the
x-axes horizontal (to the screen).
|
Look at the situation from both reference frames:
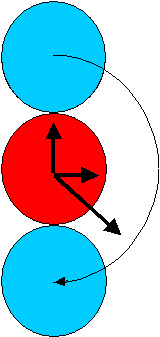

From the red reference frame perspective: The blue coin centre is initially at (0,D,0) and the blue coin rolls about the red until its centre is at (0,-D,0), and its point of contact moves from (0, D/2, 0) to (0, -D/2. 0). Meanwhile in the blue reference frame:: The red coin centre is initially at (0,-D,0), and rolls about the blue until its centre is at (0,D,0), and its point of contact moves from (0, -D/2, 0) to (0, D/2 0). That is, on both coins the point of contact has moved through 180 degrees, so that one coin is sitting on top of the other, both with the same heading as before. |