The Coin Problem
A Blue Coin is sitting on top of a red coin. Both coins have milled edges. We show the coins orientation by arrows.
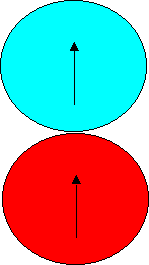
The blue coin is rolled to the right -- without slipping -- around the rim of the red coin until it is immediately below the red coin. Like so ?
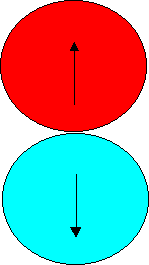
or is the blue coin now like so ?
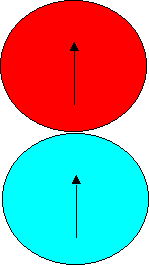
So after rolling, is the orientation of the blue coin the same as originally, or is it now inverted?
Solving the Coin Problem
Get out two coins, both the same size, and hold one still on the table, Set both coins to the same orientation, heads up say, androll the other half-way around the other without slipping.What happened? Was it what you predicted?
If YES, compare your solution to those of two scientific giants.If NO now you can stand on the shoulders of giants
I'll confess that there is no actual record of Sir Isaac Newton using the ideas in his
Principia Mathematical to solve the coin problem --
but he was appointed Master of the Mint precisely because he was the author of the Principia Mathematica
As to Einstein's Approach, in his latter years in Princeton,
he would often answer queries from high school students. These solutions -- sometimes published in
newspapers -- but mostly lost. But the solution above is most certainly done according to his methodology.
Here are two more quite different approaches:
In these two very different approaches to the Coin Problem, one is motivated by the ByPass heuristic, the other by the Reciprocity heuristic. The term heuristic means a problem-solving idea --and this term is so used on these web pagess. But we use heuristic -- in bold to denote a structured bundle of problem-solving ideas clustered about one core heuristic. This concept of heuristics was first provided in the downloadable paper, dealing mainly with tricky questions aka dragons in qualitative physics,

Harvey A. Cohen, The Art of Snaring Dragons,M.I.T. Artificial Intelligence Laboratory Memo 338,May 1975 . Terms such a schemas and p_prims have been used by later writers withsimilar meanings.
The original account of the Coin Problem is on pages 26-29 of the paper, Andrea di Sessa, "Phenomenology and the Evolution of Intuition". in Deidre Gentner and Albert L. Stevens, (Editors), Mental Models Lawrence Erlbaum Assoc., Hillsdale N.J., pp 15-33 (1983). In this paper the term p_prim is used, rather than heuristic.
This page is part of a web-site devoted to the study of qualitative thinking,with an emphasis on those problems,quite formidable and challenging,called Dragons which can be solved without having to write anything down or perform a calculation.See Dragons for an introduction to Dragons with a physics emphasis, Mostly dragons have answers like yes/no, more/the same/less,left/right, top/bottom, up/down. But also there is a category of such problems called by the philosopherof mathematics Lakatos, Monsters, wherein the problem is to debugwhat looks like a counter-example to a known solution to a problem. But if you learn that YOUR solution to a Dragon is false --the canonical wrong answer -- and become convinced that this is indeed so --then to you this first solution IS a Monster, that has to be debugged.
Enough said.




