H. A. Cohen, Covariant Wave Equations for Charged Particles of Higher Spin in an Arbitrary Gravitational Field, Il Nuovo Cimento, Serie X, Vol 52A, 1967 pp 1242-1253
Summary It is known that special difficulties are encountered in devising a wave equation to describe higher spin S≥3/2 particles in interaction with the electromagnetic field, and Buchdahl has shown that like difficulties arise when the gravitational field is introduced. We show that just as a consistent electromagnetic interaction can be introduced, so wave equations describing charged particles of spin S = 3/2 and of spin S = 2 in a universe endowed with a Riemannian metric can be devised. The paper incorporates an account of Dirac γ matrices in general relativity.
RIASSUNTO (*)
� noto che sorgono pa ri ieolari difficolt� quando si vuole impostare un'equazione d'onda che descriva particelle di spin superiore o uguale a interagenti con un campo elettromagnetico, e Buchdahl ha mostrato come simili difficolt� sorgano anche quando si introduce un campo gravitazionale. In questo articolo si fa vedere che come si pu� introdurre una interazione elettromagnetica coerente, cos� si possano trovare equazioni d'onda descriventi particelle cariche di spin S 2 o S= 2 in un universo dotato di metrica Riemanniana. Nell'articolo si includono considerazioni sulle matrici y di Dirac in relativit� generale.     (*) Traduzione a cura della Redazione.

The most recent citation of this 1967 publication is this paper on the arXiv preprint registry: [General Relativity and Quantum Cosmology] submitted Wed, 2 Aug 2017. Harold Erbin, Vincent Lahoche, Universality of tunnelling particles in Hawking radiation https://arxiv.org/pdf/1708.00661.pdf [gr-qc]

1967

H. A. Cohen^* and J. Smith^**, The C-Conserving Decay Modes η → π⁰e⁺e^- and η → π⁰μ⁺μ^-
* Mathematical Physics, University of Adelaide
** Institute for Theoretical Physics, State University of New York at Stony Brook
The C-conserving decay rate for η → π⁰μ⁺μ^- is of second order in the fine structure constant. A knowlege of the matrix elements η →γγ and γγ → e⁺e^- is sufficient to find the imaginary part of the matrix element η → π⁰μ⁺μ^- from unitarity. The real part of the matrix element can be found from dispersion relations. Recent theoretical estimates ⁽¹⁾ of the decay rate for η → π⁰e⁺e^- have assumed an interaction ηπ⁰F_μνF_μν for the ηπ⁰γγ amplitude.⁽²⁾ However, this interaction leads to the result that the decay rate into one π⁰ is proportional to the square of the mass of the leptons. The rate is therefore much larger for muons⁽³⁾ than for electrons, whereas the contrary conclusion is reached using the simple phase space argument. (which supposes a constant matrix element). One way to modify this result is to note that the C-conserving decay amplitude is decomposible into two invariant amplitudes: the first corresponding precisely to the S-wave interaction given above and the second to the P-wave interaction included in ηπ⁰P_αP_βF_αμF_βμ where P is the η four momentum. In this paper we adopt the second interaction leading to a calculation that is parallel to the calculation⁽³⁾ by the second author based on the first interaction. We calculate both the η → π⁰e⁺e^- and η → π⁰μ⁺μ^- decay rates

1968

H. A. Cohen, Vacuum polarization in the Lee and Yang theory of charged spin one , Il Nuovo Cimento A Series 10 21 Luglio 1968, Volume 56, Issue 2, pp 467-478 Summary: The radiative correction, to ordere 2, to the photon propagator in the Lee and Yang theory of charged spin-one bosons, is calculated in a dispersion-theoretic manner. Some general aspects of the ξ-limiting formalism are discussed. A useful matrix treatment of Lorentz tensors is presented in an Appendix.
Riassunto Calcoliamo, servendoci della teoria della dispersione, la correzione radiativa, di ordinee 2, al propagatore fotonico nella teoria di Lee ed Yang dei bosoni di spin uno carichi. Si discutono alcuni aspetti generali del formalismo ξ-limitante. In un appendice si presenta un utile trattamento matriciale dei tensori di Lorentz.

HINDSIGHT: The Dyson-Wick formalism that produced a manageable theory of elementary charged particles of spin 1/2 and zero spin simply failed to handle spin one QED. Lee and Yang attempted to develop a quantum electrodynamics of charged spin one by introducing a ξ-limiting formalism. Although no actual values were determined for this most speculative spin-1 QED, Lee and Yang proclaimed that their novel theory worked. In this paper I showed that using the Cutkosky approach to finding the (finite) discontinuities across the branch cuts in the complex momentum plane for substitution in the relevant dispersion relation. Contrary to Lee and Yang's claims of adequacy -- these integrals -- unlike those for spin zero and spin 1/2, simply diverged and the ξ-limiting process did not remove the infinities.

1969

A.J. Bracken and H. A. Cohen, Five Classes of Transformations of Dirac Spinors � The Free-Particle Dirac Equation Is Brought to �p₀-, �p₁-, �p₂-, �p₃- and �m-Linear� Forms �, Progress of Theoretical Physics, Vol 26, No 1, 1969, pp 816-831.
Abstract: The free-particle Dirac equation has two remarkable features: (1) It is linear in all four components of the energy-momentum p_μ, and also in the mass m. (2) For its solutions there are five distinct simple modes of the invariant scalar product in the momentum representation. In this paper, a theorem presented by Case is generalized and used to obtain five classes of transformations of the Dirac equation. Every transformation in a given class has two properties characteristic of the class: (1) The linearity in a corresponding one of the five quantities p�, m is maintained in the transformed equation. (In this way ``p_0-, ``p_1-, ``p_2-, ``p_3- and ``m-linear'' forms of the Dirac equation are obtained.) (2) A corresponding mode of the invariant scalar product is presented. Thus all five classes consist of canonical transformations. Included amongst the ``p_0-linear'' forms are the Foldy-Wouthuysen-Tani equation, and the one commonly attributed to Cini and Touschek, together with equations appropriate to limiting situations other than the non-relativistic and extreme relativistic ones. The ``canonical'' form proposed by Chakrabarti is of the ``m-linear'' type. Belonging to all three of the ``p<sub>1</sub>-, ``p₂- and ``p<sub>3</sub>-linear'' categories is a ``p-linear'' form of significance for large |p|.

1969

A.J. Bracken and H. A. Cohen, On Canonical SO(4,1) Transformations of the Dirac Equation, Journal of Mathematical Physics, Vol 10, No 11, Nov. 1969, pp 2024. Abstract: Certain matrix transformations of the free-particle Dirac equation are described as momentum dependemt SO(4,1) transformations. Such of these belonging to any one of five subgroups G^(α)(α=0,1,2,3,4,5) are canonical, preserving the Lorentz-invariant product in a corresponding one of five modes of expression. The Dirac equation itself is linear in all five components p_α[p_μ(μ=0,1,2,3) is the four-momentum operator, p₄=m ] of the "five-vector" p^~, and a transformation in G^(β) has the additional property that the component p_β appears linearly also in the transformed equation. The Mendlowitz and the Foldy-Wouthuysen-Tani accordingly are in G⁽⁰⁾, the SO(4) subgroup; and that proposed by Chakrabarti is in G⁽⁴⁾, the SO(3,1) subgroup associated with homogeneous Lorentz transformations. For any p<sup>~`</sup> obtained from p<sup>~</sup> by a momentum-dependent Lorentz transformation, there is a corresponding transform of the Dirac equation. Where p<sub>α</sub> appears in the transformed equation, p<sub>`α</sub> appears in the transformed equation. The ambiguities which arise in the specification of the transform leading to a given such equation are associated with the existence of a "little group" for any such p^~`.

1971

H. A. Cohen, On the Derivation of the Pryce-Foldy-Wouthuysen transformation, American Journal of Physics, Vol 39, April 1971, pp 409-412.
Abstract: A simple and instructive derivation of the Pryce-Foldy-Wouthuysen transformation is given in terms of rotations in two dimensions.

1972

H. A. Cohen, On Time Non-Special Quantum Mechanics, Acta Physica Austrica, Suppl. IX, 1972 pp 851-855.
Abstract: A reformulation of quantum mechanics is described in which the z co-ordinate is described in which the z co-ordinate has the special role with regard to the three other space-time co-ordinates that the time t has in the usual formulation.

1973.1

E.F. Carter and H. A. Cohen, The Classical Problem of Charge and Pole, American Journal of Physics, Vol 41, Issue 8, Aug 1973, pp 944-950.
Abstract: In this paper the classical dynamics of interacting electrically charged particles where one or both possess magnetic charge is reviewed. The equations of motion are obtained, and the vector constants of motion are derived. A consistent canonical formalism is developed while related aspects such as scale invariance and the geometry of the motion are also discussed.

1973.2

H. A. Cohen, On the Dirac Monopole Potential, Prog. Theor. Phys. Vol. 50 No. 2 (1973) pp. 691-696
Abstract: The Grönblom-Jordan picture of the Dirac magnetic monopole is reviewed. The role of the string in a single-valued vector potential describing a magnetic monopole is demonstrated.        First Page Only

1974

H. A. Cohen and M.Z. Shaharir The Action Principle in Quantum Mechanics, International Journal of Theoretical Physics, Vol. 11 No. 5 (1974) pp. 289-303
Abstract: The Euler-Lagrange equation derived from Schwinger's action principle (1951) has been shown by Kianget al. (1969) and Linet al. (1970) to lead to inconsistencies for quadratic lagrangians of the form 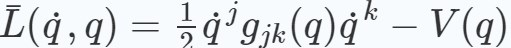except in the Euclidean case g_jk =δ_jk . This inadequacy is linked to Schwinger's specification that the variations of operators be c-numbers. We reformulate the action principle by introducing the concept of ‘proper’ Gauteaux variation of operators to find the most general class of admissible variation consistent with the postulated quantisation rules. This new action principle, applied to the LagrangianL, yields a quantum Euler equation consistent with the Hamilton-Heisenberg equations.

1974

H. A. Cohen, Is There a Quantization Condition for the Classical Problem of Charge and Pole, Foundations of Physics, Vol. 4 No. 1 (1974) pp. 115-120
Abstract: In elementary derivations of the quantization of azimuthal angular momentum the eigenfunction is determined to be exp(imφ), which is "oversensitive" to the rotation φ → φ +2π, unless m is an integer. In a recent paper Kerner examined the classical system of charge and magnetic pole and expressed Π, a vector constant of motion for the system, in terms of a physical angle ψ, to deduce a remarkable paradox. Kerner pointed out that Π(ψ) is "oversensitive" to ψ → ψ +2π, unless a certain charge quantization condition is met. Our explicandum of this paradox highlights the distinction between coordinates in classical and quantum physics. It is shown why the single-valuedness requirement on Π(ψ) is devoid of physical significance. We are finally led to examine the classical analog of the quantum mechanical argument that demonstrates the quantization of magnetic charge, to show that there is "no hope" of a classical quantization condition.